|
|
|
> . > Вернуться к списку предметов
> .. > Вернуться к списку конспектов по мат. анализу
ТЕМА: НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
1. Понятие первообразной функции.
|
Опр.1 |
Первообразной функцией F(x) для функции f(x) на интервале (a,b) называется функция F(x), дифференцируемая на (a,b) и удовлетворяющая условию: F'(x)=f(x) ∀ x О(a,b)
|
| Опр.2 |
первообразной функцией для f(x) на отрезке [a,b] называют функцию F(x), удовлетворяющую условям:
- F(x) непрерывна на [a,b]
- ∃ F'(x) на (a,b) и ∀ x О(a,b) F'(x)=f(x)
|
| Пр.1 |
(a,b)
f(x)=SinX, F(x)=-CosX ∀ x О(a,b) |
| Пр.2 |
(a,b)
|
| Пр.3 |
f(x)=1 на [0,1]
F(x)=x на [o,1) |
| Пр.4 |
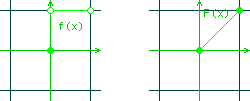[0,1]
| f(x) = |
{ |
1, x О(0,1) |
| 0, x = 0 |
F(x)=x
|
F(x) - ПО для f(x) на M =. F(x)+C - ПО для f(x) на M
(F(x)+C)'=F'(x)=f(x) =. ПО для f(x) - много |
| Th. |
Если F(x) - некоторая ПО для f(x) на M, то F2(x)=F1(x)+C, где C - некоторая произвольная константа. |
| Д-во: |
Рассмотрим ф-цию Φ(x)=F2(x)-F1(x)
Φ'(x)=(F2(x)-F1(x))'=F'2(x)-F'1(x)=f(x)-f(x)=0
Из th. Лагранжа => Φ(x)=C=const. => F2(x)=F1+C |
| След. |
Если F(x) - некоторая ПО для f(x) на M, то любая По для f(x) имеет вид F(x)+C, где C - произвольная const.
f(x)=SinX F(x)=-CosX
Φ(x)=-CosX+C
Φ(π)=2
-CosX+C=2
1+C=2
C=1
|
2. Понятие неопределенного интеграла.
| Опр. |
неопр. интегралом от ф-ции f(x) называют совокупность всех ПО-х ф-ций для f(x) на M и обозначают:
 |
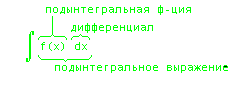f(x,y)=xy
∫xydx=y∫xdx=y
+C
|
