Конспект по ГЕОМЕТРИИ И АЛГЕБРЕ. 2 семестр.
Преподаватель: профессор Бадаев		 Версия для печати   
INDEX
РАСПИСАНИЕ
СЕССИЯ
ПРЕДМЕТЫ
СОСТАВ
ГАЛЕРЕЯ
КАРТА
АНЕКДОТЫ
ОТЗЫВЫ
ВЫХОД
НАВЕРХ

 > .. > Вернуться к списку предметов



ТЕМА: КОМПЛЕКСНЫЕ ЧИСЛА И МНОГОЧЛЕНЫ.
16.02.2002
1. Поле комплексных чисел.
Опр. Числа вида α+iβ, (α, β ∈ R) называют комплексными числами.

iÖ(-1),  i2=-1
C - комплексные числа;
R - действительные числа;
RÍC
αÎR   α+i0
α - вещественная часть комплексного числа z=α+iβ
β - мнимая часть комплексного числа z=α+iβ
Re(z)равно по определениюα   вещественная часть числа z
Im(z)равно по определениюβ   мнимая часть числа z
Опр.Комплексные числа z1=α1+iβ1 и z2=α2+iβ2 равны, если α1=α2, β1=β2
Алгебраическое представление комплексного числа z:
z=α+iβ
Геометрическое представление комплексного числа z: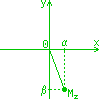
Oxy - декартова система координат.
Mz(α,β)
z=α+iβ
     1-1           1-1
z|~~~~>Mz|~~~~>0Mz
Опр. Сумма z1+z2 - это число ((α1+α2)+i(β1+β2))
Опр. Произведение αz1 (α ÎR) - это число ((αα1)+i(αβ1))
Свойства сложения комплексных чисел
  1. z1+z2=z2+z1   (комутативность сложения)
  2. (z1+z2)+z3=z1+(z2+z3)   (ассоциативность сложения)
  3. ∃ z1 ∀ z2: (z1+z2=z2+z1=z2); z1=0+i0=0
  4. ∀ z1 ∃ z2: (z1+z2=z2+z1=0); α2=-α1; β2=-β1
  5. Свойства умножения комплексного числа на действительный коэффициент те же самые, что и у умножения вектора на коэффициент.
Тригонометрическая форма комплексного числа
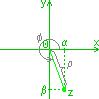z=α+iβ   α,βÎR
0x - полярная ось; 0 - полюс.
Полярные координаты точки z - это пара (ρ,φ)
ρ - расстояние 0z; ρ=ρ(0z)=|0z||z|
|z| - модуль числа z
φ - угол от направления оси 0x до луча 0z, отсчитываемый против часовой стрелки.
z=0 => угол φ неопределен
z=0 => |z|=0
α=|z|cosφ
β=|z|sinφ
z=|z|(cosφ+isinφ)
z=-Ö3 + i
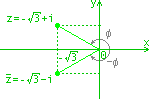|Ö3+i|=Ö(3+1)=2
φ=150°
-Ö3+i=2(cos150°+isin150°)
eiφравно по определениюcosφ+isinφ - формула Эйлера
z=|z|eiφ
Опр.z1=α1+iβ1; z2=α2+iβ2; z1z2равно по определению(α1α2-β1β2)+i(α1β2+β1α2)
Опр. Число равно по определениюα-iβ называется сопряженным к числу z
Свойства сопряжения и моуделй (СРС)
    ____  _   _
  1. z1±z2=z1±z2
Сайт управляется системой uCoz